Quicknotes on Syllogism

Solving Syllogism Problems

Solving Syllogism problems can be hard if you don’t know the correct way, in Syllogism we have a two Assumption Statements followed by Logical Conclusion and we have to tell which logical conclusion(s) is(are) true based on the Assumption Statements.Go through this page to get an idea on How to Solve Syllogism Questions Quickly. Let us try to understand what is Syllogism with an example –

Statements(Assumptions/Premises)

S1: All doctors are surgeons.

S2: Some chemists are doctors

Conclusions

1. Some chemists are surgeons.

2. All surgeons are chemists.

Statements might not make logical sense, we have statements saying all pen are papers and all papers are erasers, which defies laws of nature, in such cases focus on the answer and forget logical laws.

Rules for solving Syllogism Questions

There are three different methods to solve Syllogims which are –

  1. Verbal Method
  2. Venn Diagram Method
  3. Tick and Cross Method

Verbal Method –

It’s a very simple one, try to make logical deductions in your mind from Assumptions (Premises) and match which conclusion is true.

Example –

Premises

  • All tigers are cats.
  • All cats are animals.

From these, we can easily conclude that since all tigers are necessarily cats and all Cats are necessarily animals. So, all tigers are animals.

Conclusion- All Tigers are Animals.

Venn Diagram Method –

There are four categories to remember to solve using Venn’s Diagram.

Rule 1 Syllogism:

Statement – All A’s are B
Example – All Mangoes are Fruits

Conclusions that can be made out.

Conclusion 1 – Some A’s are B or Some Mangoes are Fruits
Conclusion 2 -Some B’s are A or Some Fruits are Mangoes.

Now, the first conclusion may confuse you as we said All A’s are B’s and then we are concluding some A’s are B’s.

In Syllogism its not wrong to say some A’s are B when you have a statement as All A’s are B’s, as –

Some A’s are actually B or Some Mangoes are actually fruit. This is not a wrong information

Rule 2 Syllogism:

  • Statement – No A is B
  • Example – No Tomatoes are Fruits

This has a direct conclusion are No A is B

 

Rules for solving Syllogism Questions
Rule 3 Syllogism:

These have these possible conclusions –

  • Statement – Some A’s are B
  • Example – Some men are Engineers

 These have these possible conclusions –

  1. Conclusion 1 – Some A are not B
  2. Conclusion 2 – All A are B.
  3. Conclusion 3 – All B are A
  4. Conclusion 4 – All A are B and all B are A.

Now, Conclusion 1 is clear as if some men are Engineers then some may not be engineers (Check Image for Conclusion below Conclusion 2 two is a case when we for a sample set, only Engineers maybe allowed to do engineering. Similar of Conclusion 3 For Conclusion 4 both men and Engineers are same sample set i.e Sample Set(Men) = Sample Set(Engineers)

Some Quick Tricks to Solve Syllogism

& Rules –

  • All+All = All
  • All+No = No
  • All+Some = No Conclusion
  • Some+All = Some
  • Some+No =  Some Not
  • Some+Some =  No Conclusion

If the conclusion provided in the question is in “Possibility” case then you must proceed as per the following rules:

  1. If All A are B => Some B are Not A is a Possibility.
  2. If Some B are Not A => All A are B is a Possibility.
  3. If Some A are B => All A are B is a Possibility & All B are A is a Possibility.

Note: In a few questions drawing diagrams may be very cumbersome as you may have to draw 4 diagrams depending upon the possibilities arriving specially Rule 3 which has 4 possibilities.

Ticks and cross solves the problem of not having to create many diagrams.

Ticks – They denote defined set
Cross – They denote undefined set

Defined Set – When all the elements of that set have to be known in order to define a particular premise.

Undefined Set – If all the elements of a set need not be known in order to make a particular statement

Each Syllogism Premise must be one of the four –

Universal AffirmativeAll As are Bs.
Universal NegativeNo As are Bs.
Particular AffirmativeSome As are Bs.
Particular NegativeSome As are not Bs.

Some Rules by Aristotle to solve Syllogism :

Checking if Conclusion is possible or not –

  1. When Counting total premises and conclusion they should be 3
  2. If we encounter a situation where in both the premises are negative then no conclusion can be achieved.
  3. If we encounter a situation where in both the particular(some is used) are negative then no conclusion can be achieved.
  4. The middle term (common term of both premises) must be distributed at least once.

Checking nature of conclusion – 

  1. If one premises is particular then conclusion will definitely be particular.
  2. If one premises is negative then the conclusion will be negative.
  3. A term that is not distributed in the premises cannot be distributed in the conclusion.
Learning with an Example –

Premises –

  • All parallelogram are four sided.
  • Some parallelograms are square.
Rules for solving Syllogism Questions

Mentioned below are some statements followed by a conclusion in the options. Take the given statements to be true, even if they contradict to the commonly known facts, and determine the conclusions that logically follow the statements.

1. Statement:
1. All boys are girls.
2. Some girls are students

Conclusion:
1. All girls are boys
2. Some girls are not students.

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

Since both, the conclusions contain the term girls so neither of them can follow.

Hence option D is the correct one.

Correct option: D

2.Statement:
1. All men are women.
2. All women are kids.

Conclusion:
1. All men are kids
2. Some men are not kids

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

By looking at the statements, it is clear that since all men are women and all women are kids, we can say that all men are kids.
Therefore the only conclusion I follow the statement.

Therefore one can say that option A is the correct one.

Correct option: A

3.Statement:
1. All Orange are fruits.
2. No Banana is Apple.

Conclusion:
1. No Banana is a fruit.
2. Some Banana are fruits.

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

Here, the first statement is a universal positive statement, so the middle term Orange is forming the predicate is distributed twice. So the conclusion cannot be universal. Therefore, either conclusion I or II must be followed.

Correct Option: C

How to Solve Syllogism Questions Quickly - (Venn Diagram method)

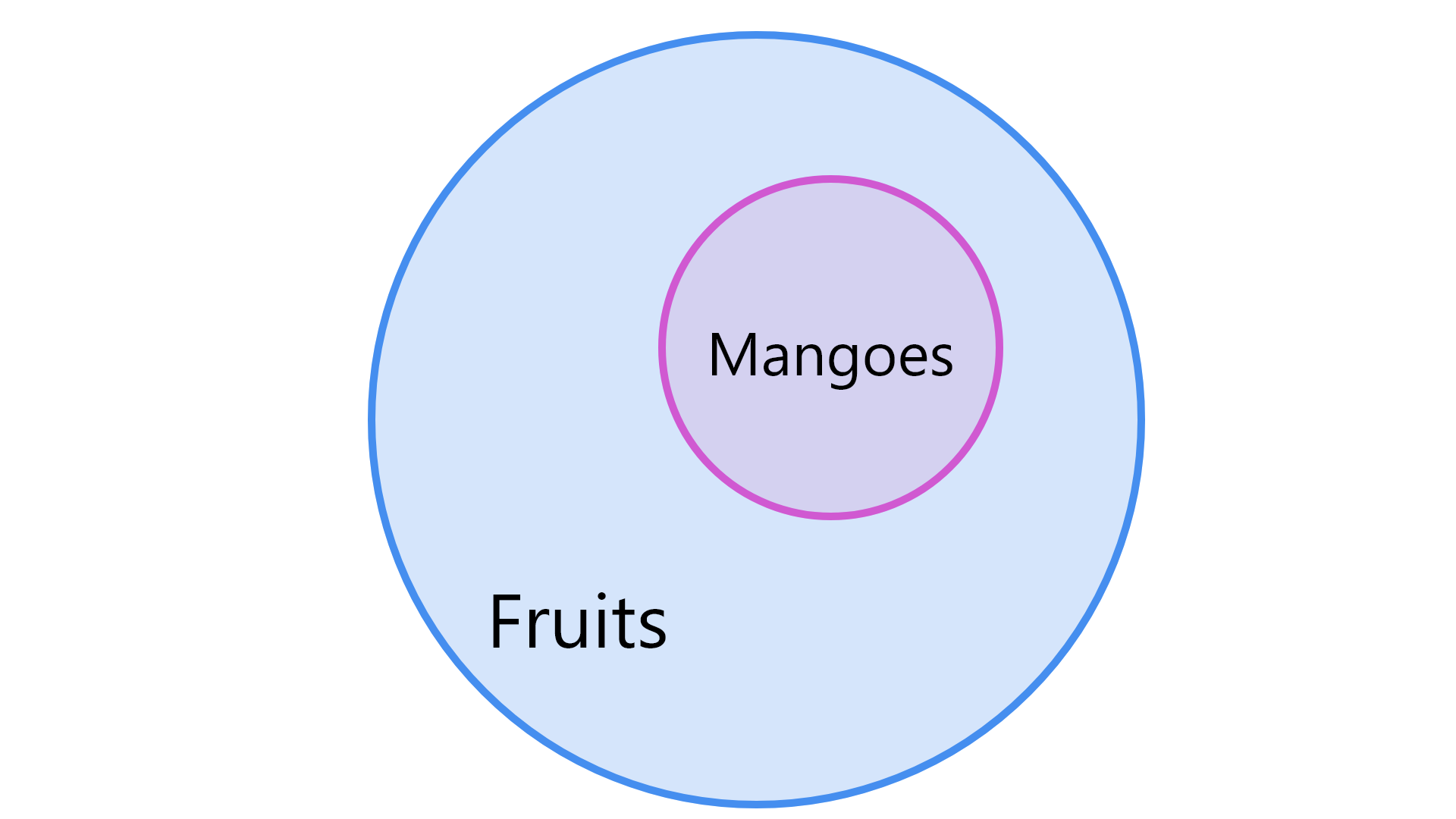
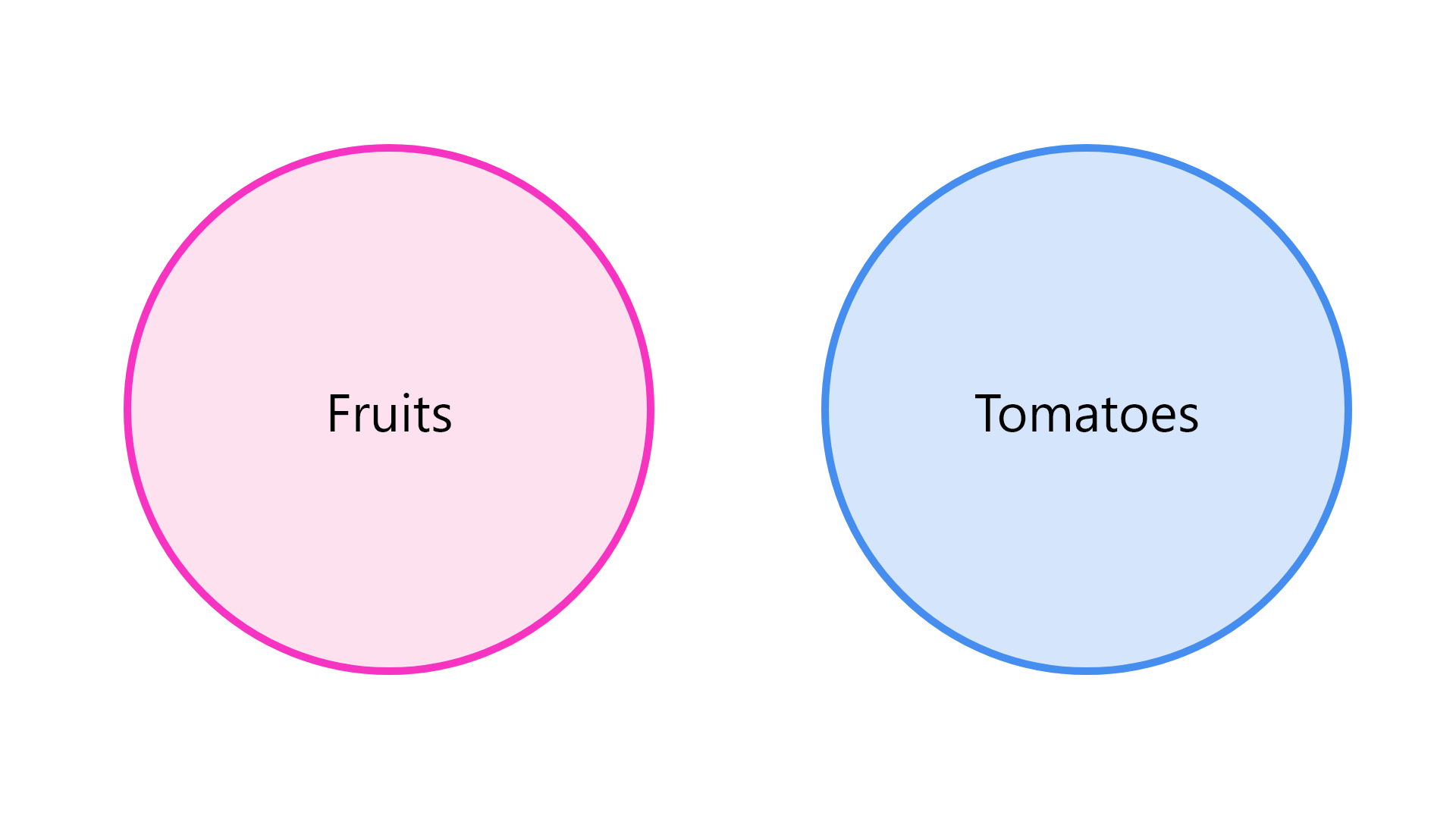
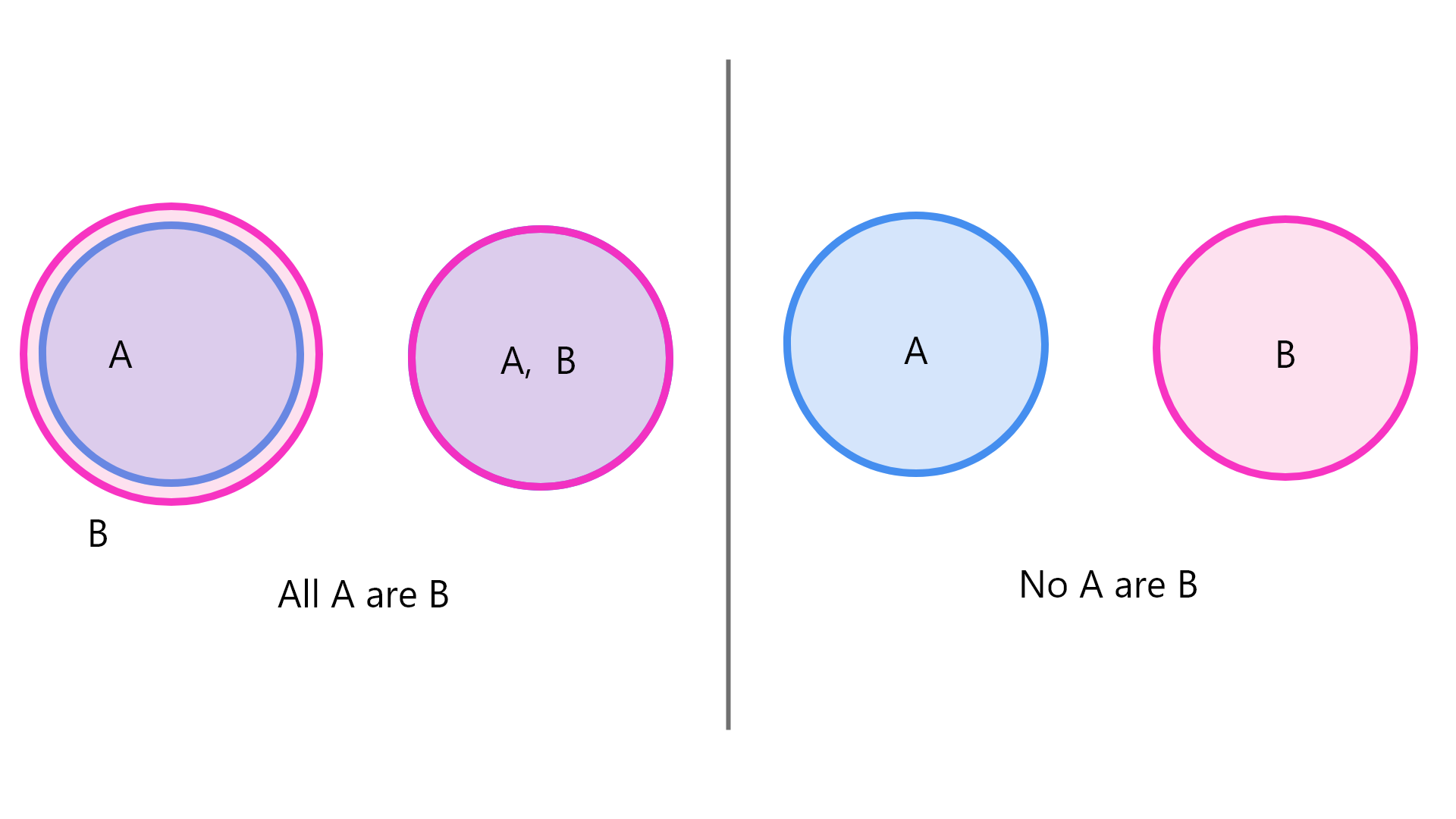
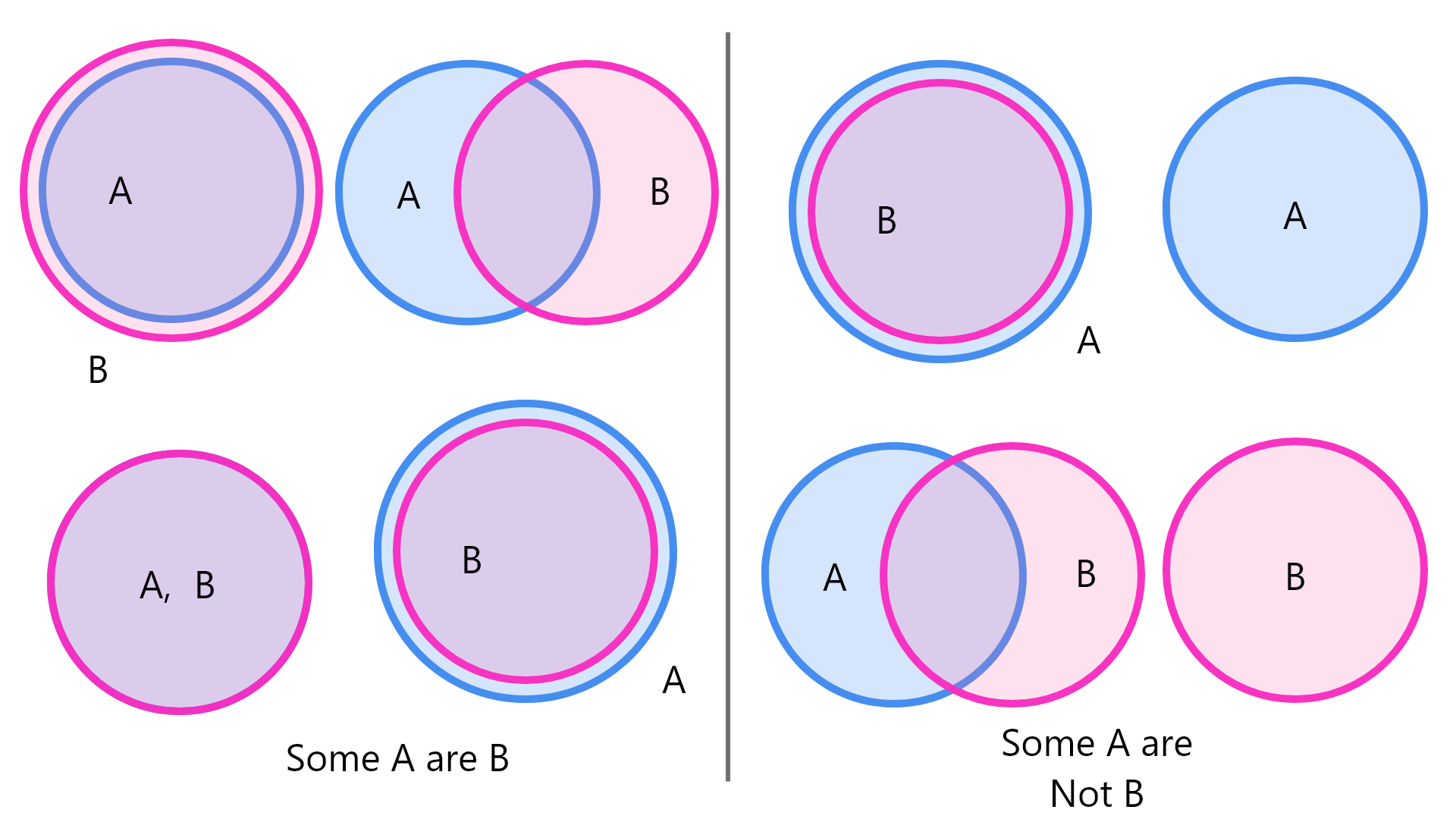
The most easier way to solve syllogism questions is using the help of the Venn diagrams.

All we have to do is, read the given statements and accordingly draw the Diagram step by step, by the given statements, and eventually derive a logical solution with the help of the final diagram.

Examples :

1) Statement:
1. No pen is book.
2. No scales are pens.

Conclusion:
1. All scales are book
2. Some scale is pen.

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

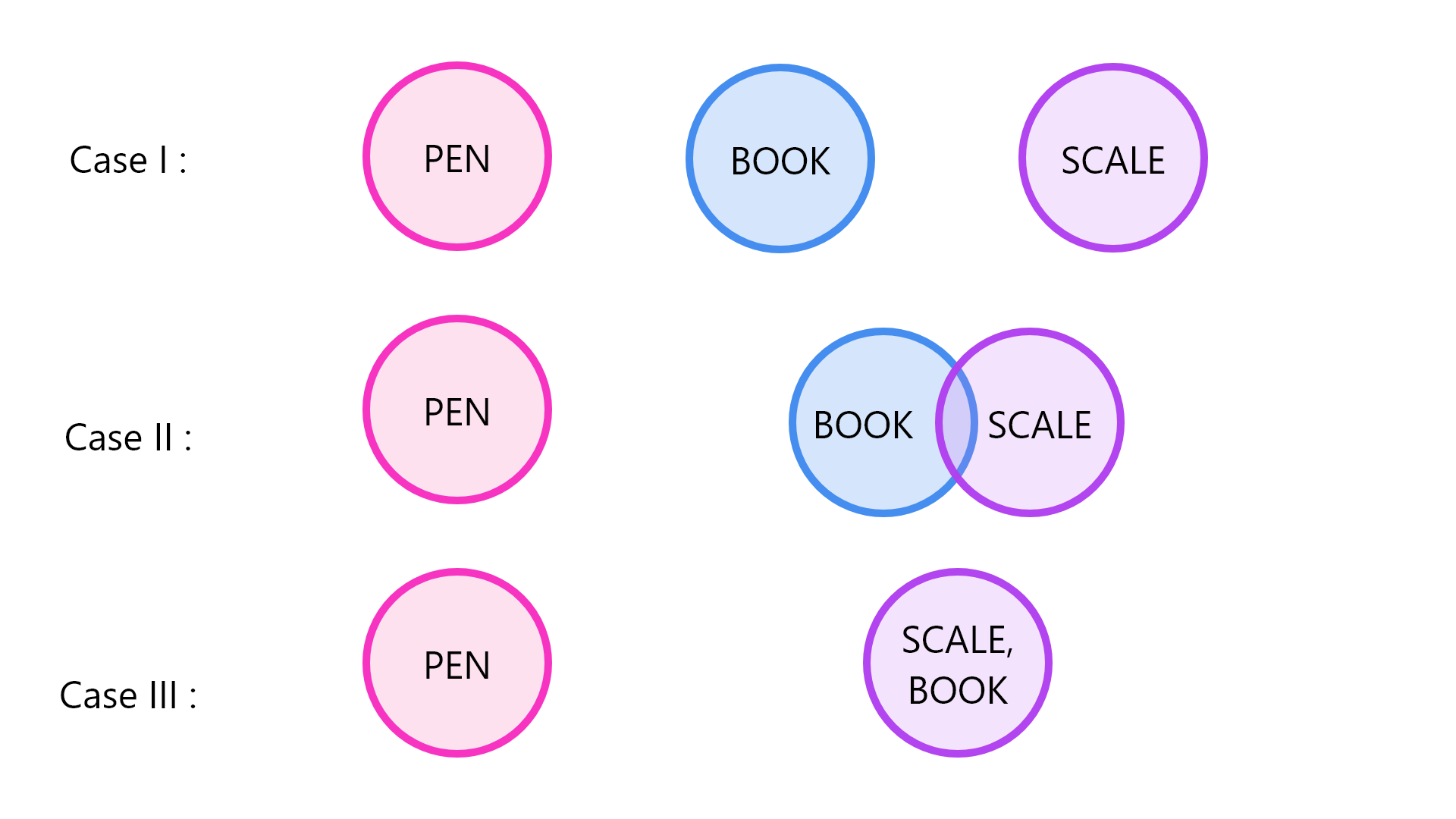
There are 3 possible cases.

Since “ No pen is book” The diagram of pen and book do not have any overlapping. Hence, they are apart. According to the second statement, since no scales are pens, the diagrams of scales and pen do not overlap.

Case 1: If no scales are pen, one possibility is there can be no scales which is book also.

Case 2: There can be scales which is also bool. Hence a part of scales and book overlap with each other.

Case 3: All coats can be a scales, as there is no statement which says this combination is not possible.

Therefore option D is the correct one.

Correct option: D

2.Statement:
1. Some Jhon is Jill.
2. Some Matheu is Jhon.

Conclusion:
1. Some Jill is Matheu
2. No Jill is Matheu

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

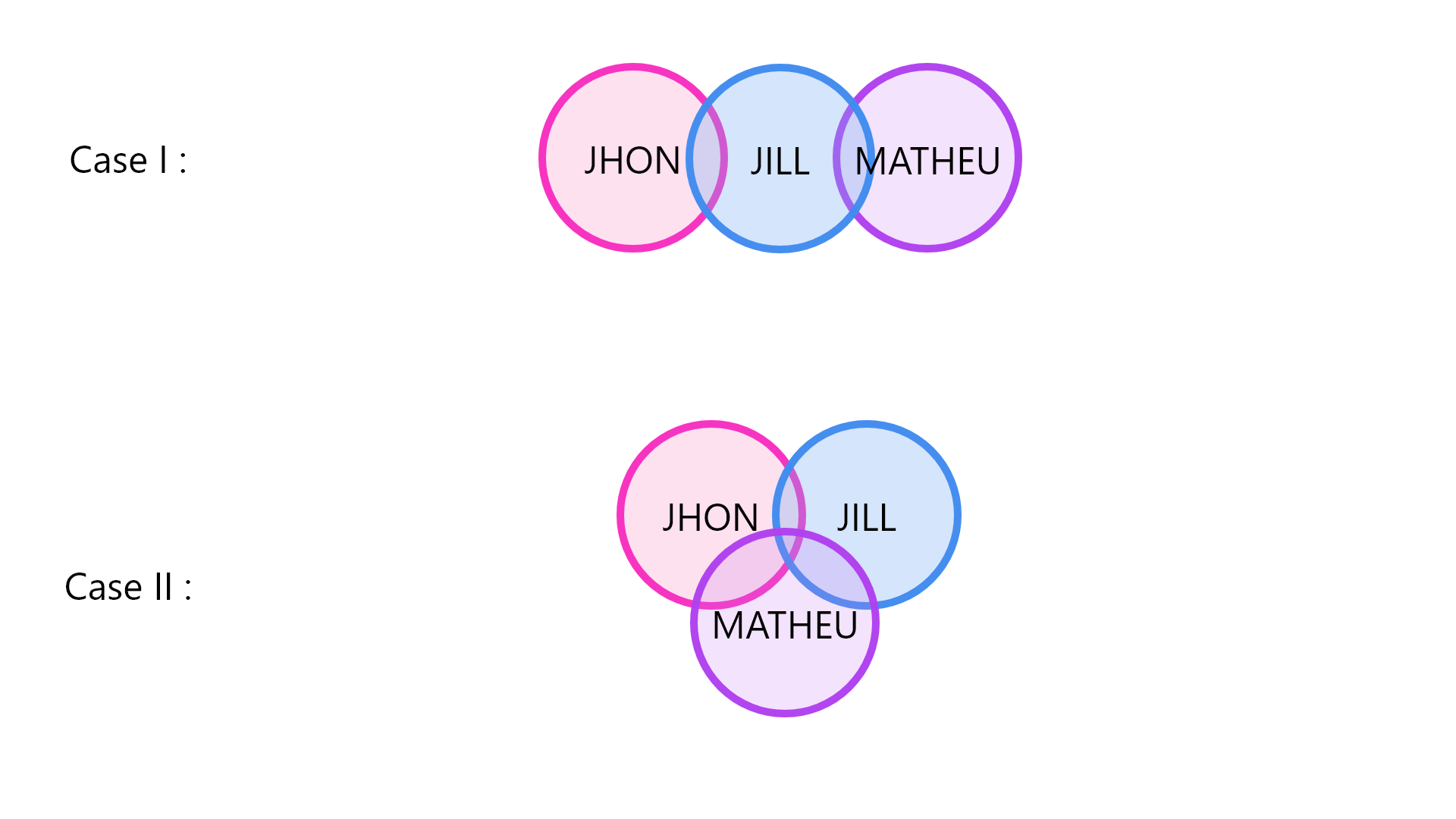
By looking at the above diagram, it is evident that either conclusion I or conclusion II follow since the conclusion is forming a complementary pair.

Hence option C is the correct one.

Correct option: C

3.Statement:
1. All men are strong.
2. Anil is a man.

Conclusion:
1. Anil is strong
2. Anil is not strong.

Options:

A. The only Conclusion I follows

B. Only Conclusion II follows

C. Either conclusion I or Conclusion II follows

D. Neither conclusion I nor Conclusion II follows

Solution:

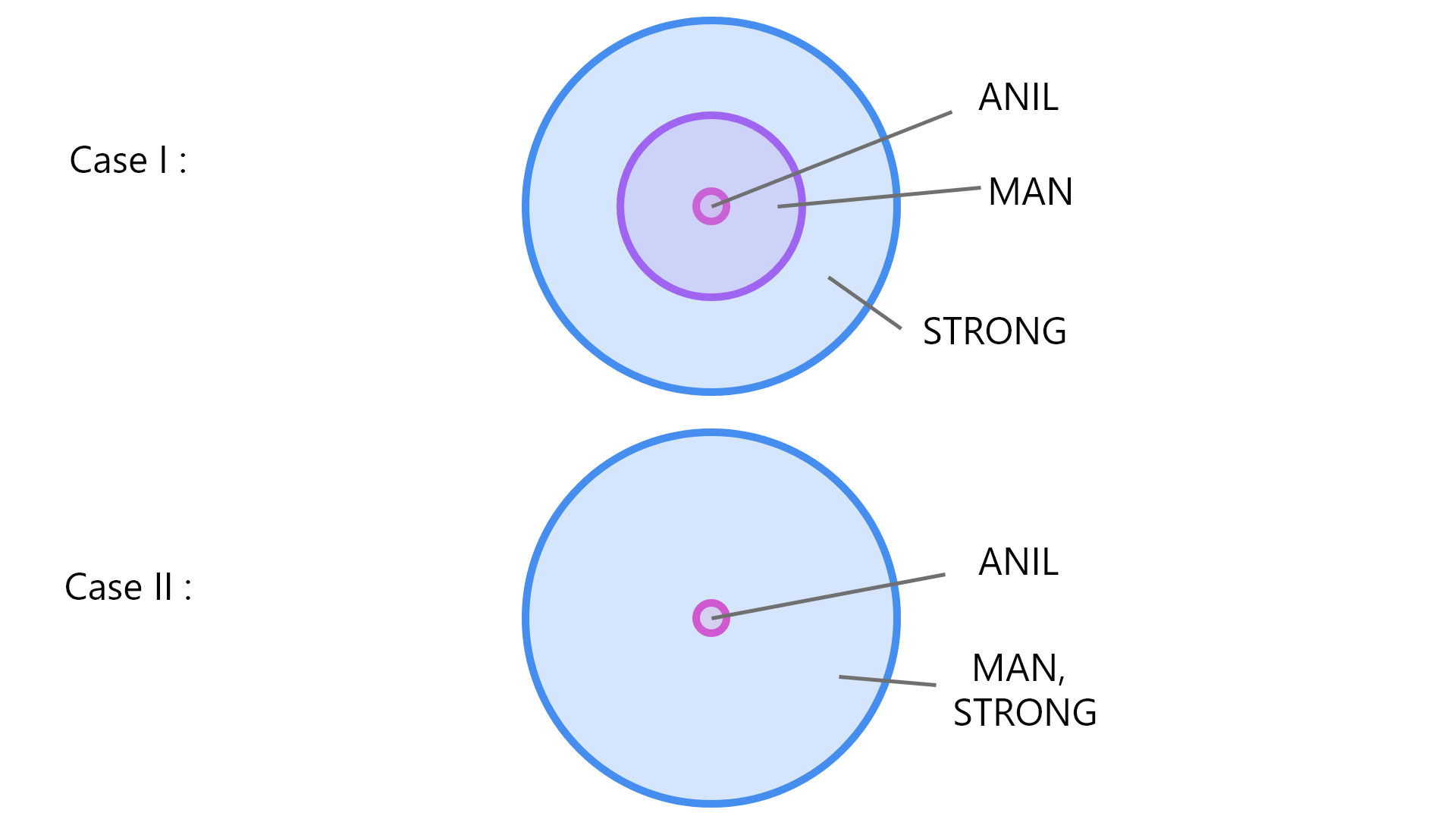
In the first case, the statement “ All men are strong “ the Venn diagram of men is inside the Venn diagram of strong. In the second statement, since Anil is a man, the Venn diagram representing Anil should be inside man. In the second case, the only difference is, the first statement “ All men are strong “ the Venn diagrams of men and strong are overlapping with each other. Because that’s another possibility. Since Anil is men, it is represented inside it. Observing both the cases, we can agree that the conclusion given “ Anil is strong “ is true from both the case.

Hence, Correct option is A

Correct Option: A