-
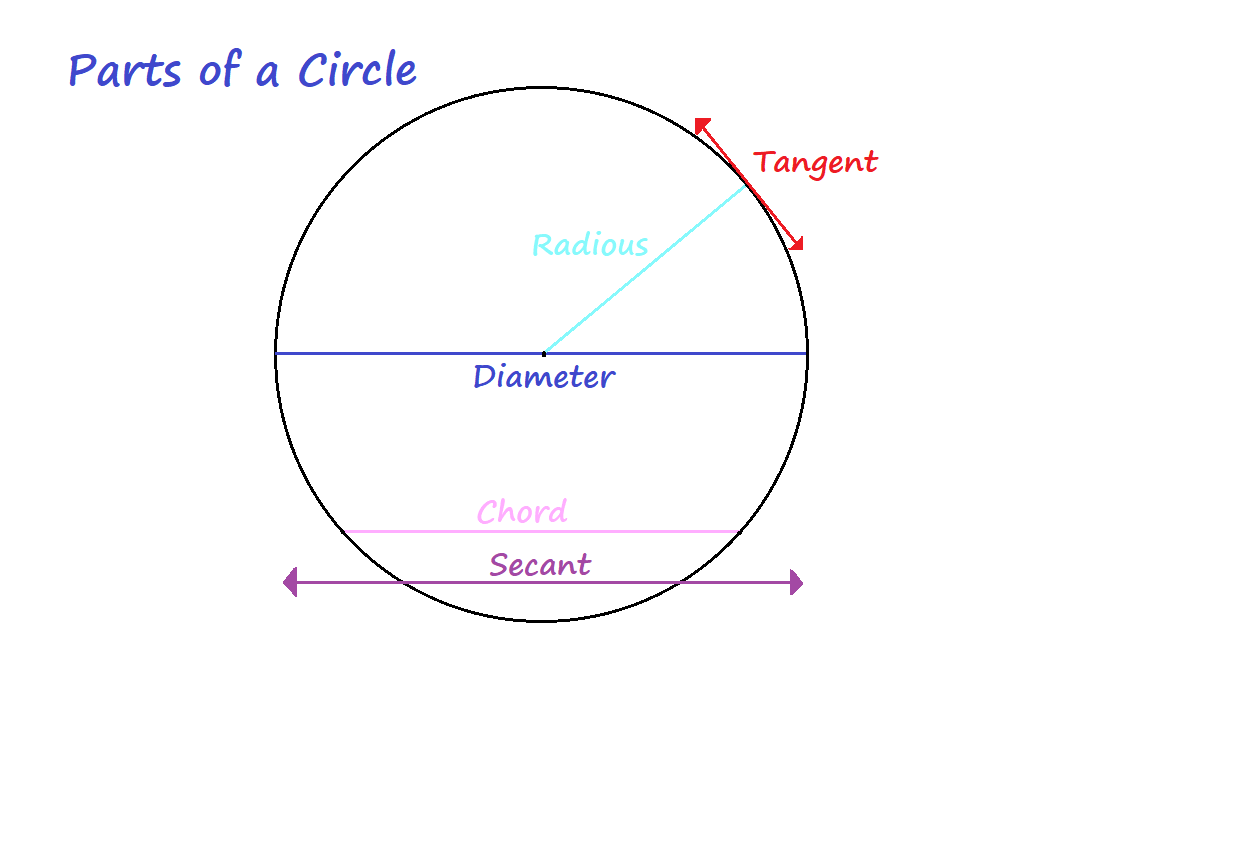
Different parts of Circle :
- Centre
- Circumference
- Chord
- Radius
- Diameter
- Minor segment
- Major segment
- Interior part of the circle
- Exterior part of the circle
- Arc





Now, let's count the number of unit squares in the figure given. How many squares can you see ?
There are 15 squares in total.
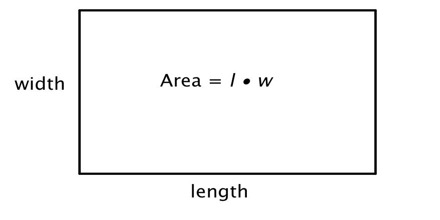
We have already learned that area is measured in square units.
Since the unit of this rectangle is "inches," the area is measured and written in square inches.
Thus, the area of the rectangle = 15 square inches.
Now, the formula to calculate the area of a rectangle is $Length$ × $Breadth$. Alternatively, we can write this formula as $\sqrt{(Diagonal)^2-(Breadth)^2} $.
So, Area of a Rectangle $= Breadth$ x $\sqrt{(Diagonal)^2-(Breadth)^2} $.

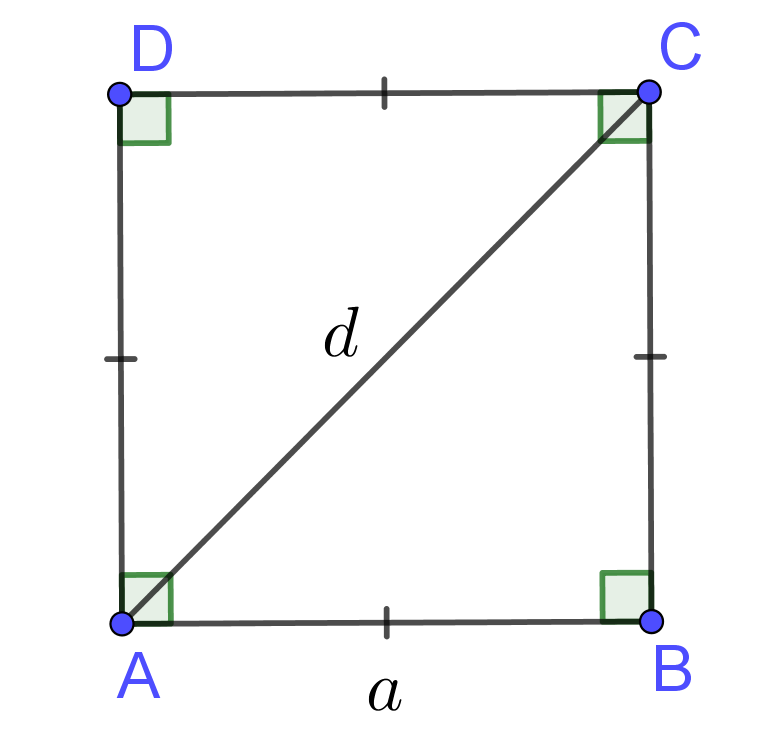
The formula for the area of a square when the sides are given is:
Area of a square = $Side$ × $Side$ = $a^2$


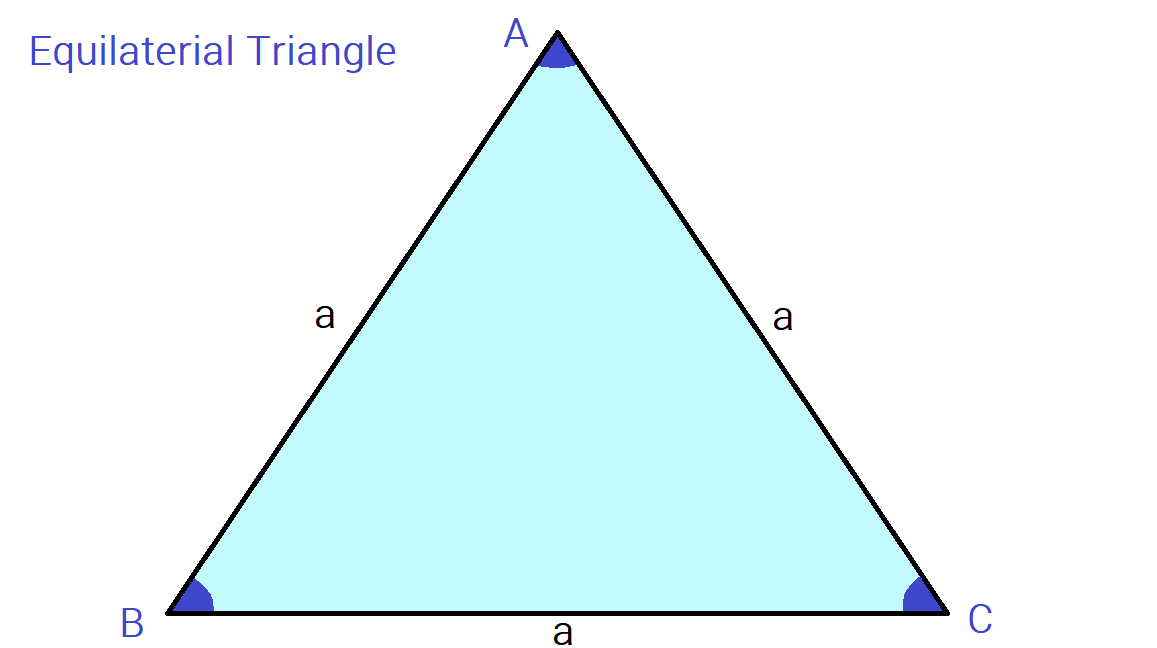
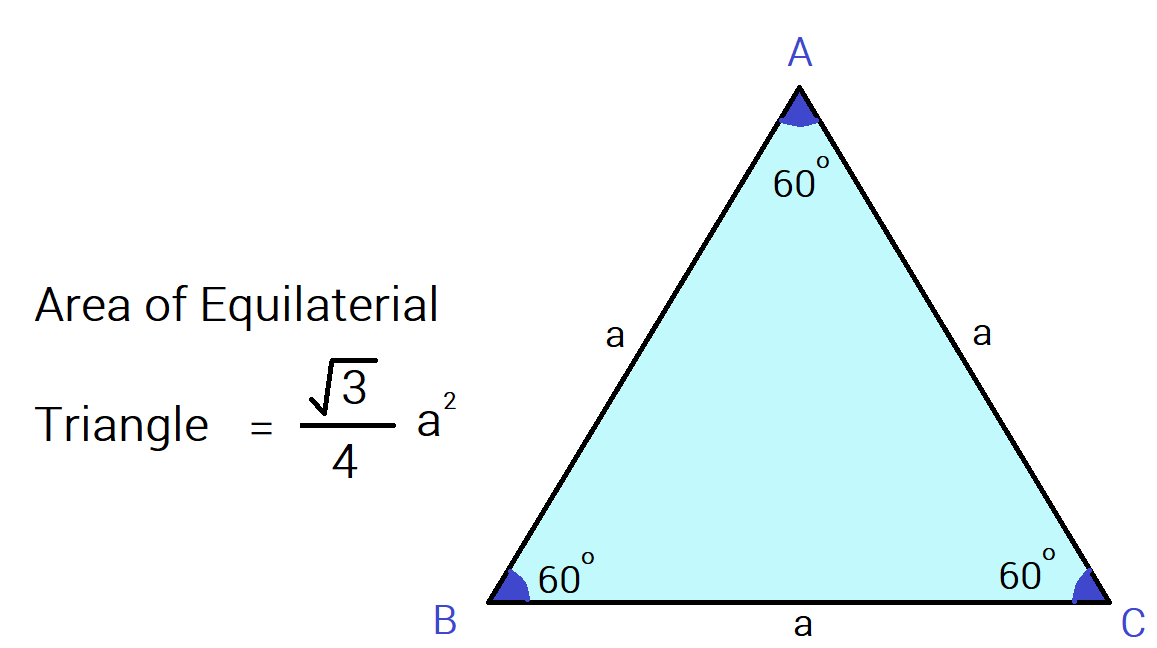
An equilateral triangle is a triangle where all the sides are equal. The perpendicular drawn from the vertex of the triangle to the base divides the base into two equal parts.
To calculate the area of the equilateral triangle, we need to know the measurement of its sides.
Area of an Equilateral Triangle = $A = \frac{\sqrt{3}}{4} × side^2$
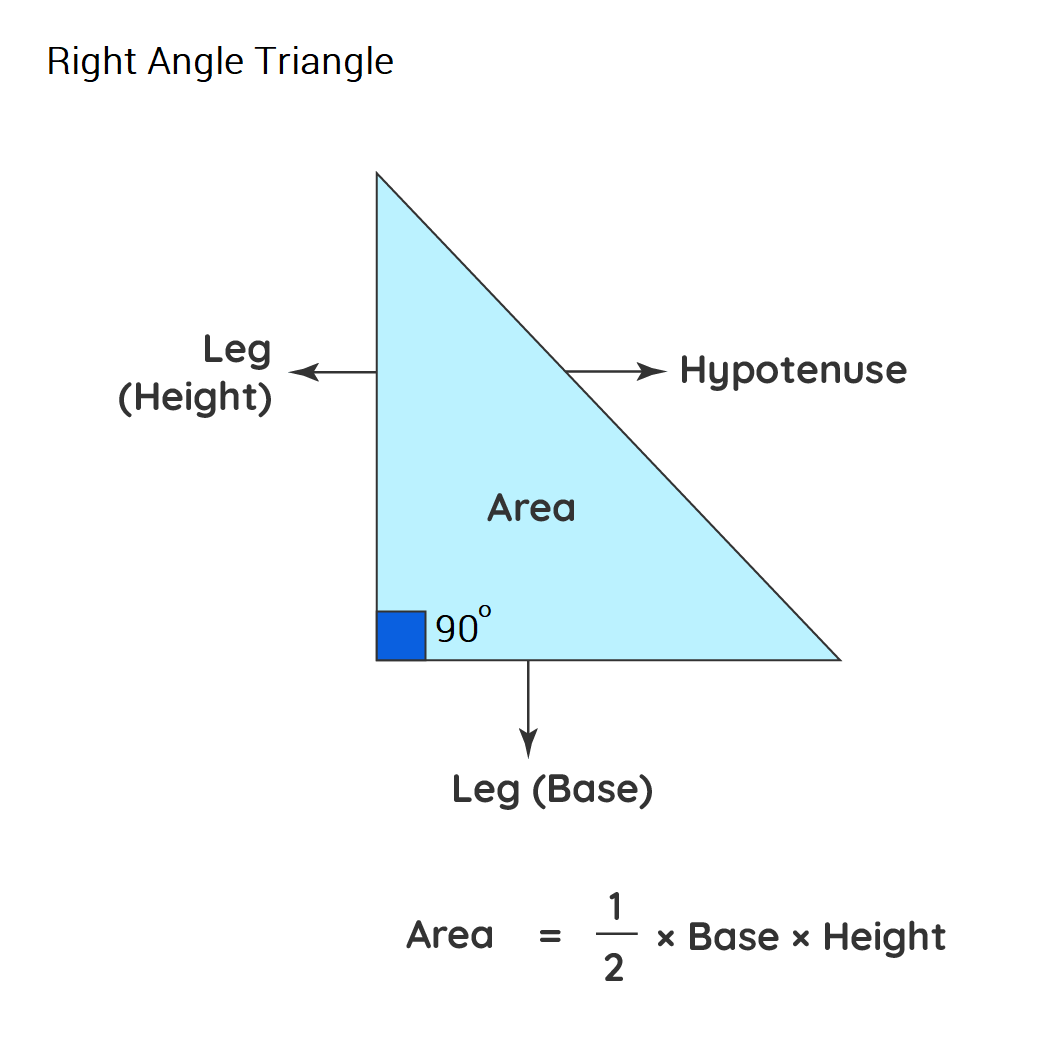
A right-angled triangle, also called a right triangle, has one angle equal to 90° and the other two acute angles sum up to 90°.
Therefore, the height of the triangle is the length of the perpendicular side.
Area of a Right Triangle = A = $\frac{1}{2}$ × Base × Height
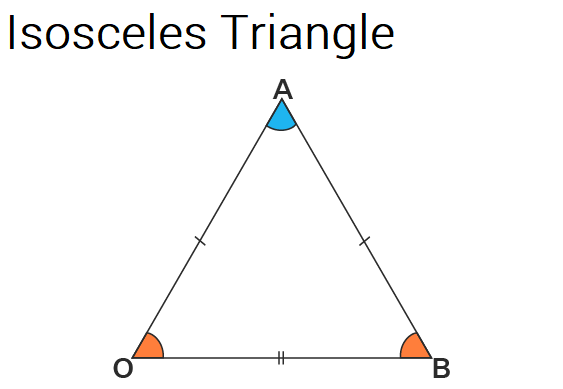
An isosceles triangle has two of its sides equal and the angles opposite the equal sides are also equal.
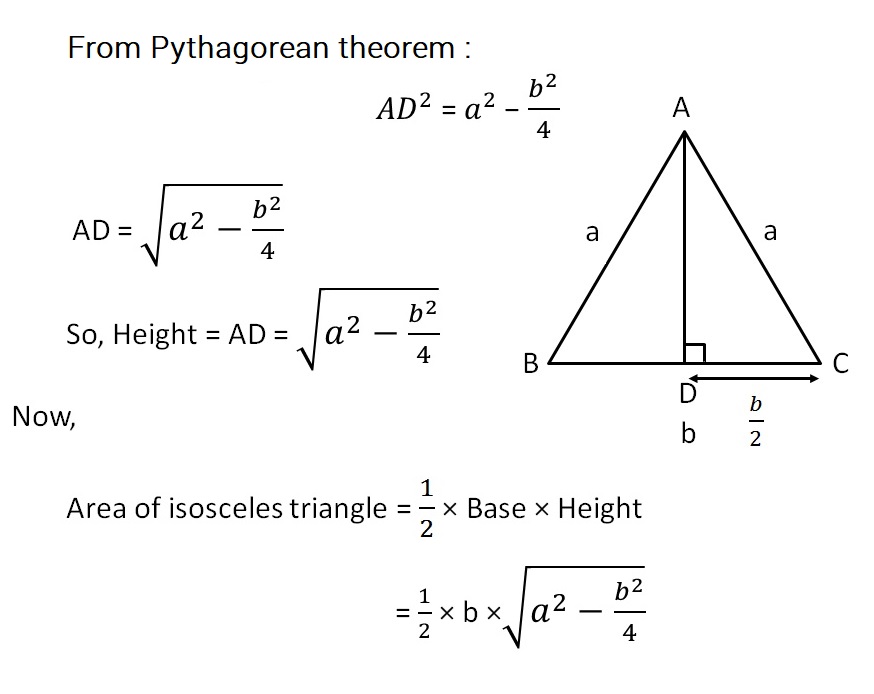
Area of an Isosceles Triangle = A = $\frac{1}{4}b\sqrt{4a^2−b^2}$
where $b$ is the base and $a$ is the measure of one of the equal sides.
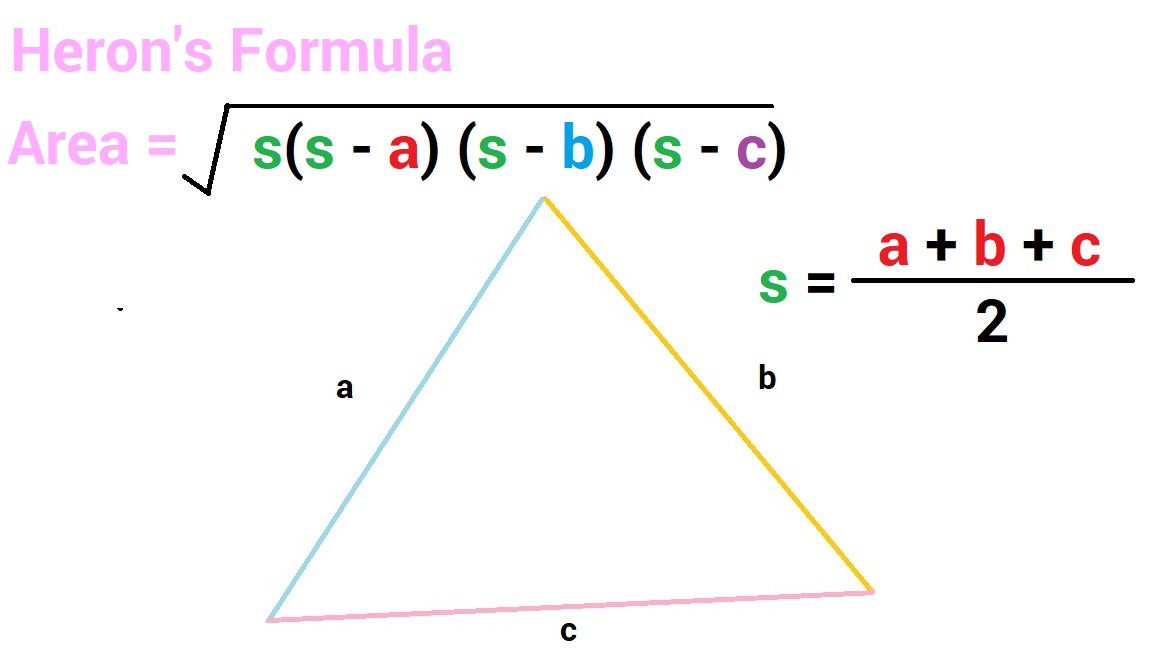
Observe the table given below which summarizes all the formulas for the area of a triangle.
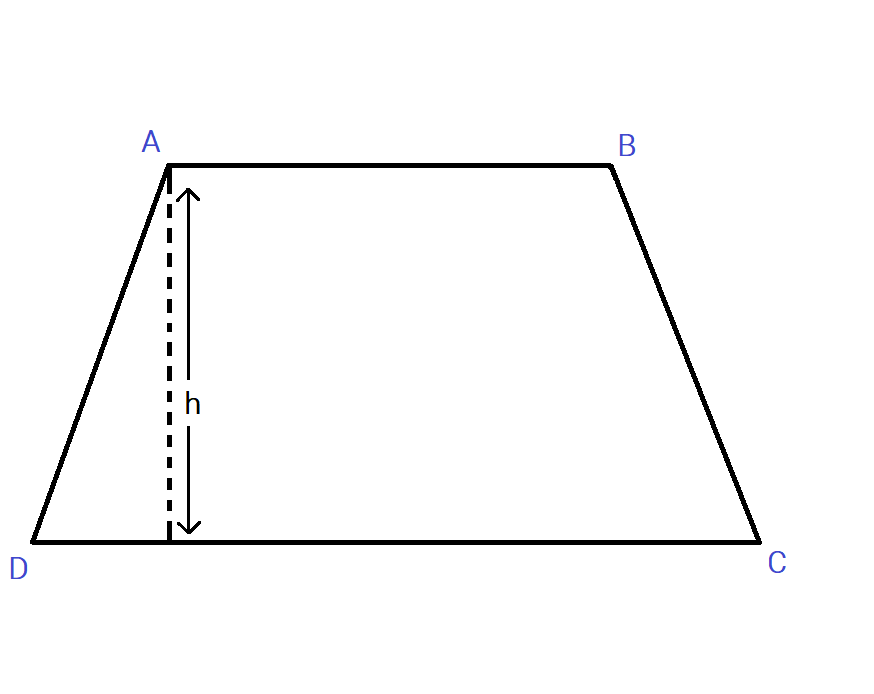

A trapezium is a type of quadrilateral that has one pair of parallel sides(generally referred to as bases).
The other pair of sides of a trapezium can be non-parallel and are known as legs.
The area of a trapezium is the total space covered by a trapezium in a two-dimensional plane.


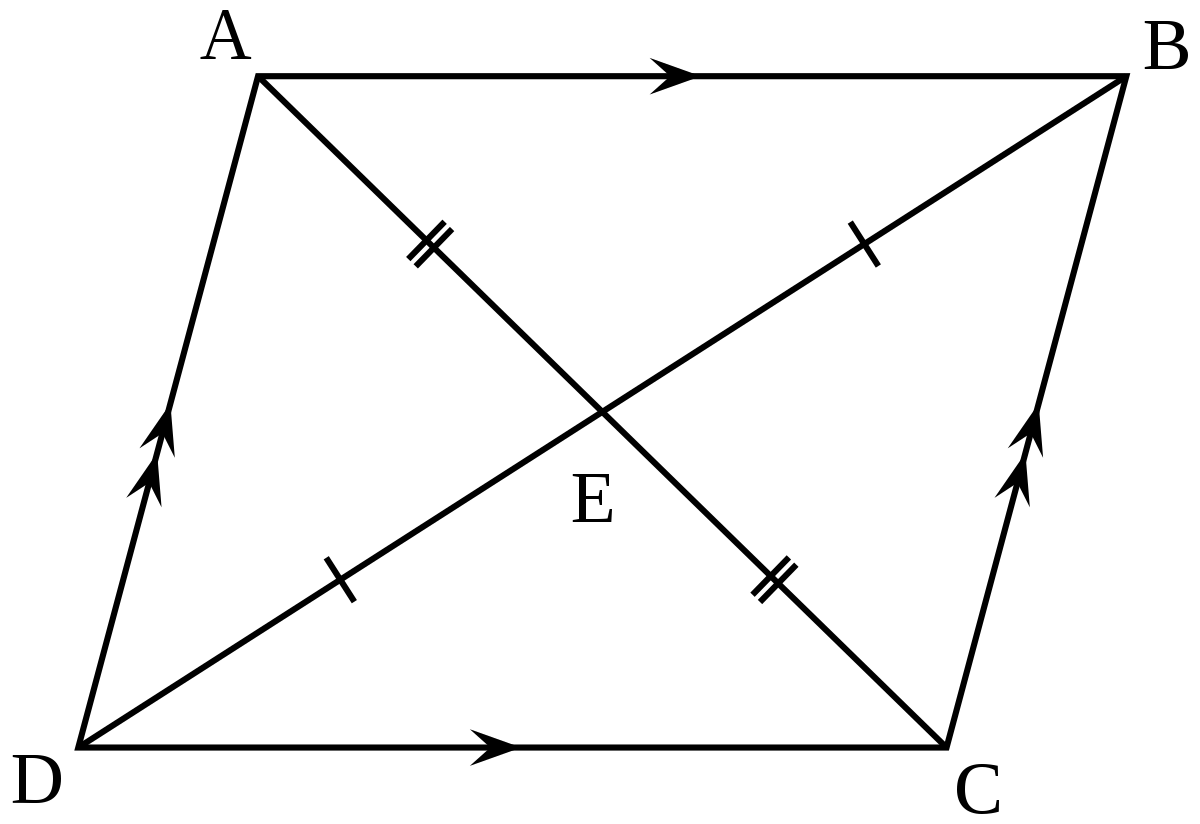
The area of a rhombus can be defined as the amount of space enclosed by a rhombus in a two-dimensional space.
Rhombus is a parallelogram with the opposite sides parallel, the opposite angles equal, and the adjacent angles supplementary.
The following properties are used to define a rhombus.
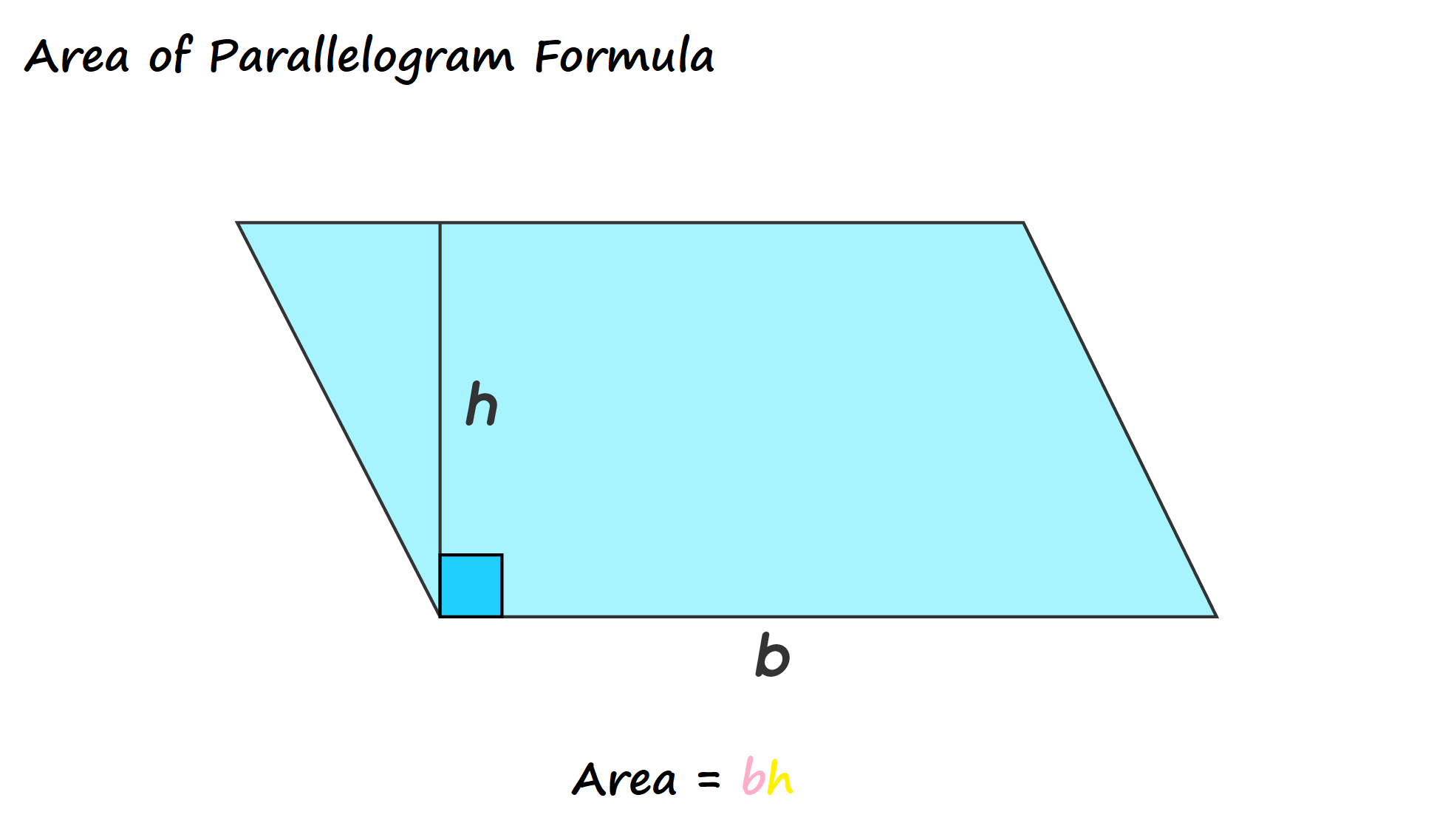
It is the region enclosed or encompassed by a parallelogram in two-dimensional space.
A parallelogram is a four-sided, 2-dimensional figure with:
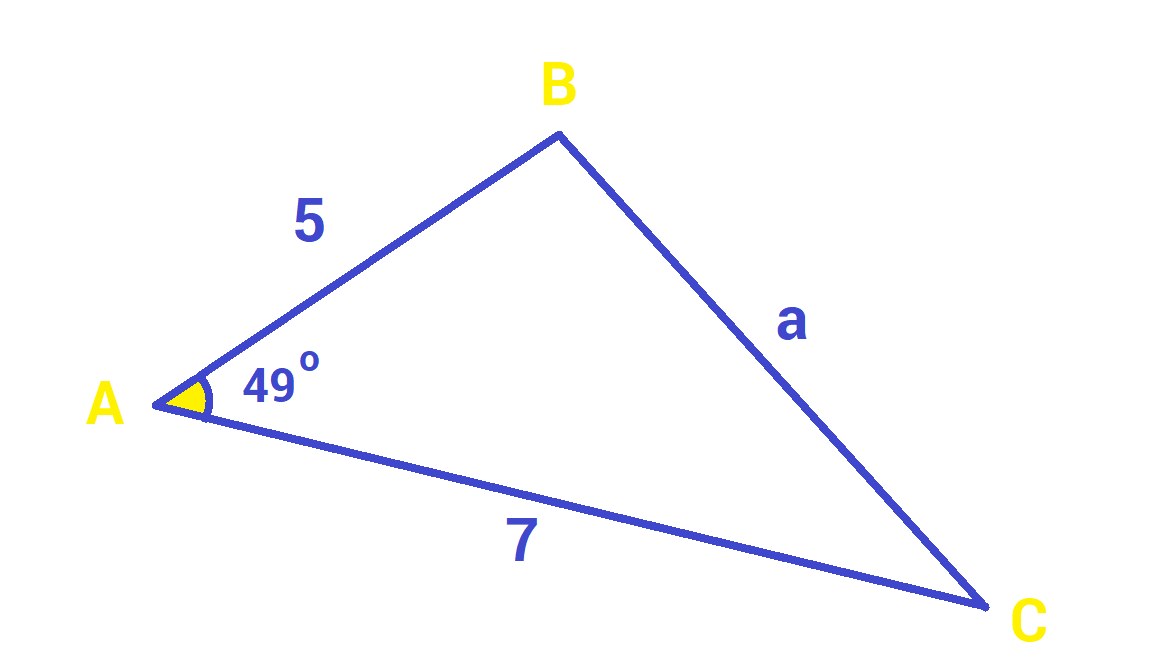
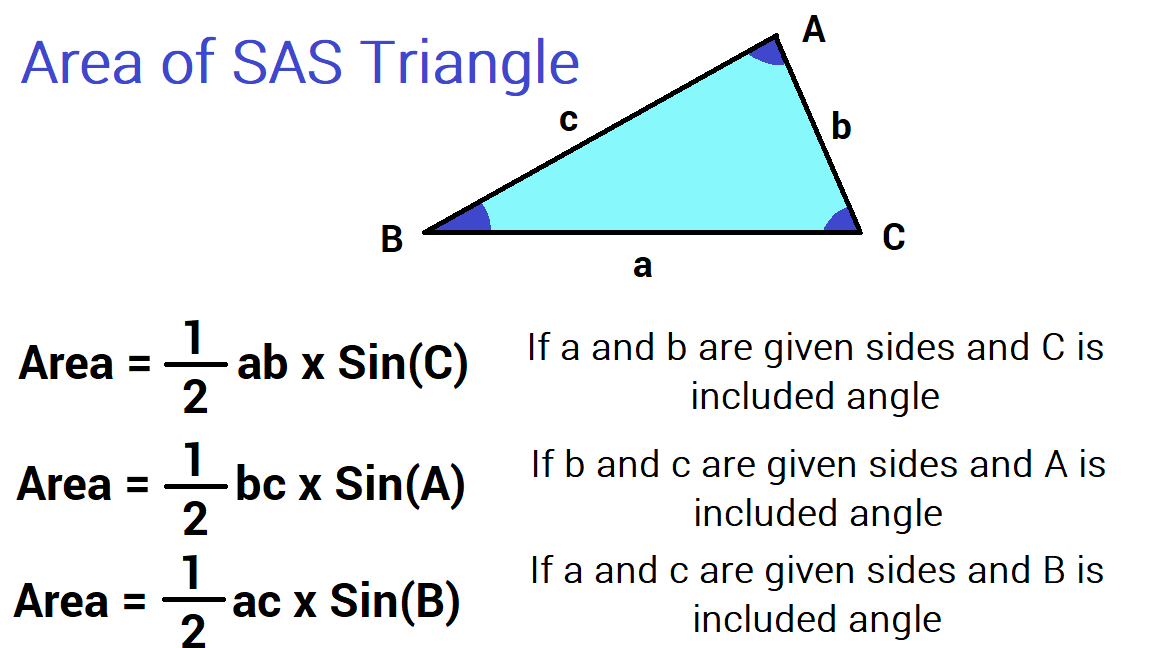
The area of a parallelogram can also be calculated without the height if the length of adjacent sides and angle between them are known to us.
We can simply use the area of the triangle formula from the trigonometry concept for this case.
Area = ab sin (θ)
where,
The area of a circle is the space occupied by the circle in a two-dimensional plane.
A circle is a collection of points that are at a fixed distance from the center of the circle.
For a circle with radius $r$ and circumference $C$:

Different parts of Circle :
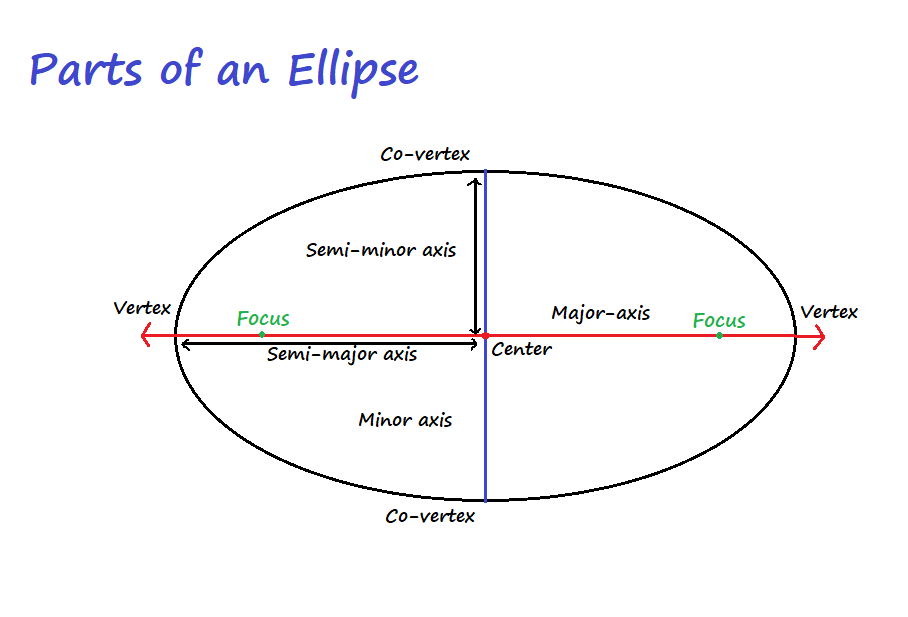
Ellipse is a 2-D shape obtained by connecting all the points which are at a constant distance from the two fixed points on the plane..
he fixed points are called foci. F1 and F2 are the two foci.
As an ellipse is not a perfect circle, the distance from the center of the ellipse to the points on the circumference is not constant.So, an ellipse has two radii.
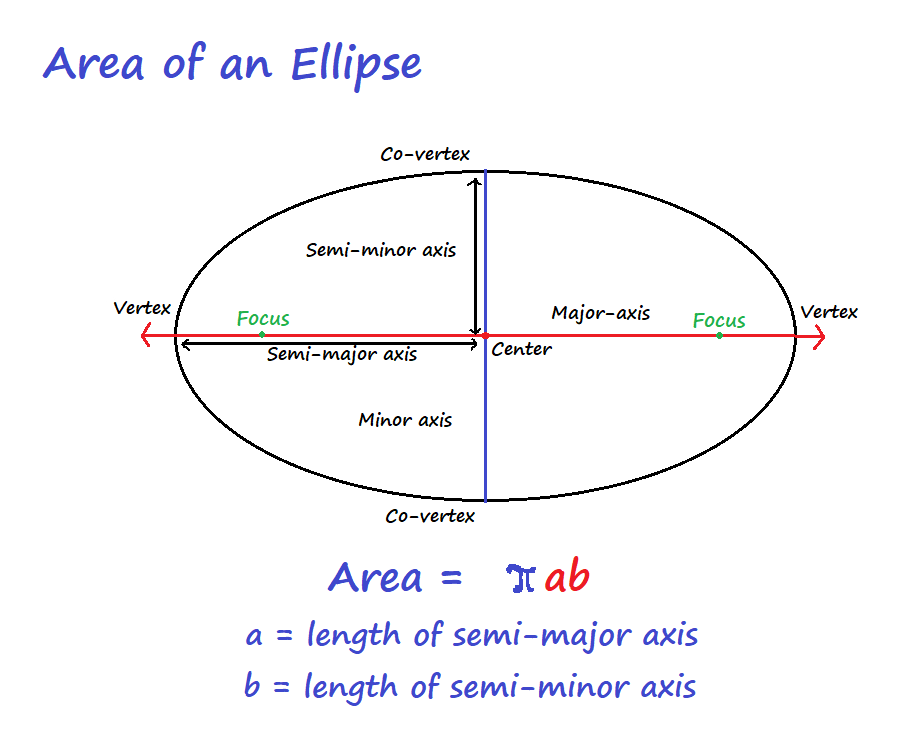
We can calculate the area of an ellipse using a general formula, given the lengths of the major and minor axis.
The formula to find the area of an ellipse is given by,
Area of ellipse = π a b
where,