Aptitude
Introduction to Percentage

-
Percentage means “per one hundred.” It expresses a number as a fraction of 100.
We use the symbol % for percentage: x% means x out of 100, i.e. $\dfrac{x}{100}$.
Common uses: grades, discounts, interest rates, population statistics, and comparisons.
-
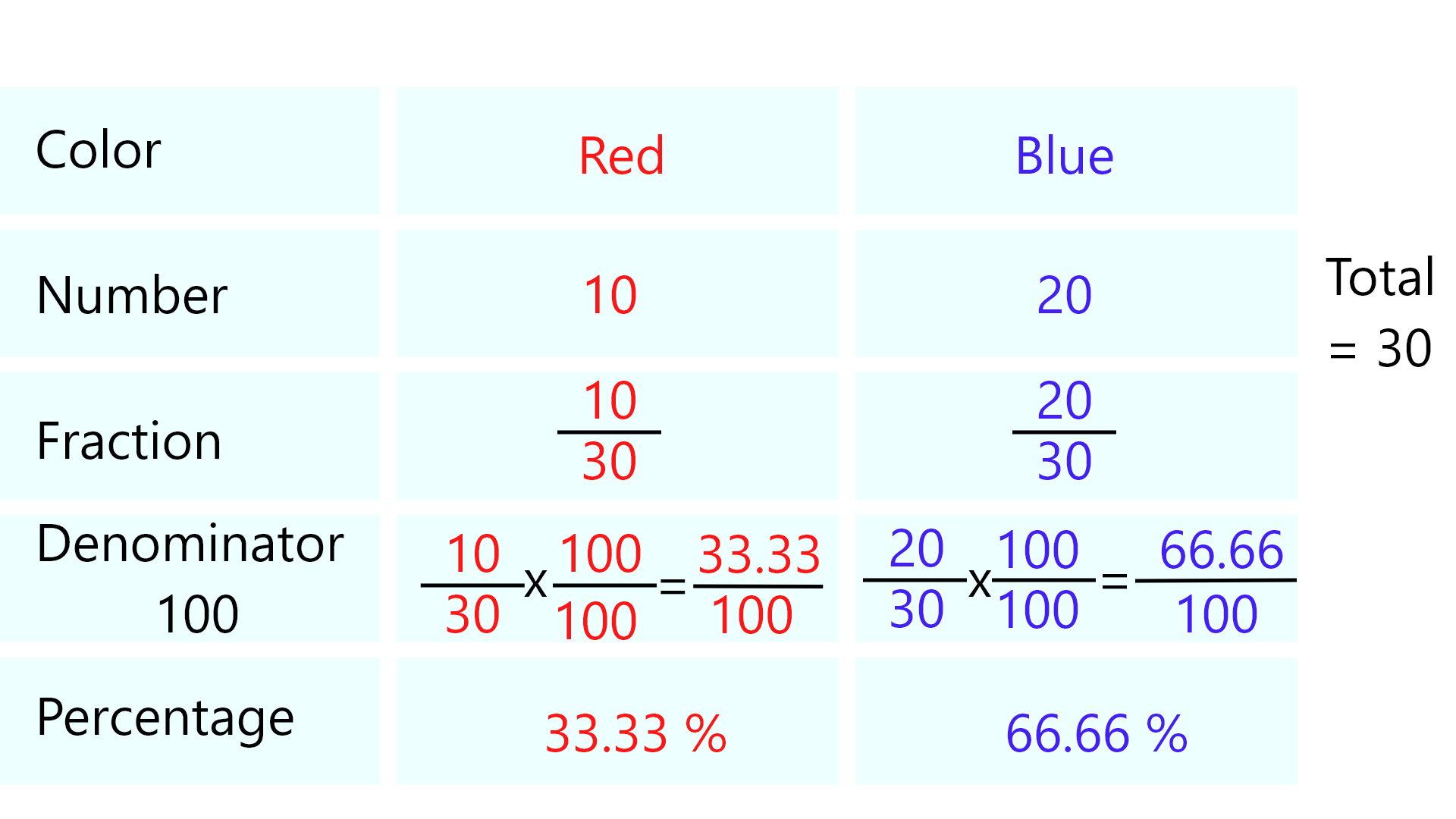
Percentage = (Part / Whole) × 100 — this is the basic formula to find what percent a part is of a whole.
-
Two simple methods:
- Unitary method: find 1% then multiply — e.g. 1% of 250 is 2.5, so 12% is 12×2.5 = 30.
- Make denominator 100: convert fraction to denominator 100 (scale numerator/denominator) and read off percentage.
-
Example formula: $\text{Percentage} = \dfrac{\text{Value}}{\text{Total}} \times 100$
-
Examples:
- What percent of 80 is 20? $\dfrac{20}{80}\times100 = 25\%$.
- Convert 0.37 into percentage: $0.37\times100 = 37\%$.
- To convert percent to decimal: divide by 100. (e.g. 15% → 0.15)
- To convert decimal to percent: multiply by 100. (e.g. 0.08 → 8%)
- To convert fraction to percent: compute fraction × 100. (e.g. $\tfrac{3}{4}\times100 = 75\%$)
Percentage increase when value rises from $A$ to $B$:
Percentage Increase = $\dfrac{B - A}{A} \times 100$
Percentage decrease when value falls from $A$ to $B$:
Percentage Decrease = $\dfrac{A - B}{A} \times 100$
Note: successive percentage changes are multiplicative. e.g., increase by 10% then by 20% gives factor $(1+0.10)(1+0.20)=1.32$ → overall 32% increase, NOT 30%.
- 10% of a number = divide by 10.
- 5% = half of 10% (divide by 20); 25% = quarter (divide by 4).
- 1% = divide by 100; 0.5% = divide by 200.
- To find 17% of X = X × (20% − 3%) = X×0.20 − X×0.03 (use decomposition to simplify mental math).
Find 12% of 250: 10% of 250 = 25; 2% = 5; total = 25 + 5 = 30.